12/09/2022 | The challenges of the 21st century require systems thinking and modelling at regional and global scales, for example with regard to weather extremes, marine heat waves, global change-induced impacts on tropical coasts and their communities, coral reefs, mangroves or ecosystem services in general. Models can support the prediction and development of adaptation efforts in a long-term framework. In the series 'Research in short', Professor Jan O. Haerter describes the challenges of modelling equilibrium in an ecosystem.
What was the initial question of the study?
In our study, we took a close look at a theoretical model that has been used as a standard for decades to investigate the state of equilibrium in an ecosystem. So-called random matrices are tables whose coefficients are random numbers. If one uses this method, then one assumes that the equilibrium state of a dynamical system – in our case an ecosystem – can be characterised by linear stability analysis and that certain quantities are actually independent of each other.
What exactly does that mean?
An ecosystem, i.e. the populations of all species, can be in a stable or unstable equilibrium. When interactions between the different components of an ecosystem are balanced, an ecological equilibrium is achieved. If the system is stable, even minor disturbances, such as fluctuations in temperature or available nutrients, cannot harm it and the populations return to equilibrium after a certain time.
In an unstable system, however, the disturbance makes it such that the equilibrium can no longer be established, but the species start a potentially complicated transition to a completely new equilibrium – often associated with the extinction of individual species. Then a tipping point is reached and the ecosystem has fundamentally changed. We want to better understand precisely the latter and use models to make predictions about when and how the ecological balance of a system can falter or even collapse.
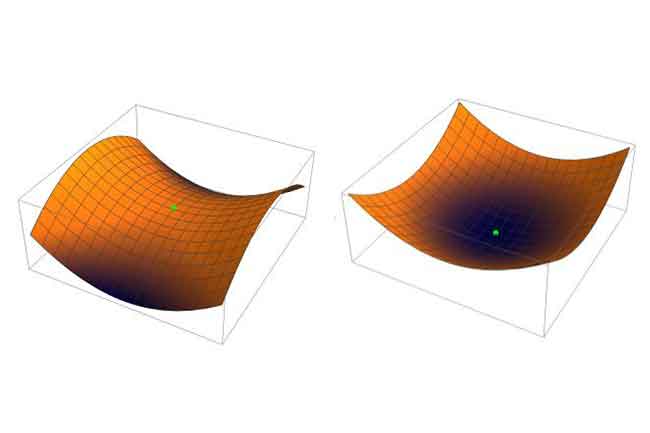
Figure: Schematic representation for two species (green dot). One spatial direction is stable, the other unstable with respect to disturbances (left side). Both spatial directions are stable (right side).
And the previously used calculation method of random matrices is no longer suitable?
That is precisely the question. Our study takes a critical look at the established approach of random matrices. We ask whether it is at all permissible to describe (ecological) equilibrium by applying random matrices. The description of a complex system consisting of many different variables, which can correspond to e.g. species populations, goes back to the pioneering work of Robert May, 1972. May realised that mathematical knowledge about random matrices can be applied to complex systems – under the crucial assumption that these random matrices represent the equilibrium state of a complex system in the first place. (May, Robert M. "Will a large complex system be stable?." Nature 238.5364 (1972): 413-414.)
What does your apporach entail?
The balance in an ecosystem is based on self-regulation. In our analysis, we first 'allow' an ecosystem to organise itself by gradually 'adding' species to an existing ecosystem and interacting with it – for example, as a a predator of a prey species or as a virus attacking a bacterium. We use established equations of population dynamics for this, namely the generalised Lotka-Volterra equations. These put the species into concrete relationships with each other.
At the beginning of our computer modelling, we start with a single species and add others in turn, so that 'artificial' ecosystems are gradually created in theory, sometimes containing ten species and more. It is important that we always ensure that the species reach an equilibrium that is sustainable, i.e. stable. If this is not the case, we supplement an extinction of 'weak', i.e. insufficiently adapted/fit species until equilibrium is established among all remaining species. In this way, we can gradually create an artificial system with hundreds of thousands of plausible ecosystem states.
And now how do the random matrices come into play?
We now ask in each case whether these different states of ecosystems could be described by random matrices and draw a comparison. When using random matrices, the stability of an ecological equilibrium is described by their so-called eigenvalues (see figure). The eigenvalues describe the temporal development of the ecosystem: with a positive eigenvalue, even a small deflection from equilibrium is amplified, while with a negative eigenvalue, small deflections are basically reduced. The eigenvalues form an interesting geometric structure, as they all fall within a circular area in the complex number space. The density of the complex numbers is statistically constant within this circle. This simple geometric circle structure now allows us to compare in a quite concise way the eigenvalues of 'our' previously theoretically created – and in the course of an assumed evolution adapted – ecosystems. The result is clear: the ecosystems that have evolved show a bimodal distribution of eigenvalues. In this bimodal distribution, the eigenvalues cluster at two opposite extremes, whereas in a circle they would tend to lie in the middle range.
What does this reveal?
We conclude that actually evolved ecosystems go through a complex 'filter', namely the evolutionary process, until they finally reach a self-organised geometric distribution of eigenvalues that deviates strikingly from the geometry of random matrices. Our study will therefore hopefully provoke a rethinking of the role of random matrices as a null model for ecosystem stability.
The study is about theoretical models and calculations. What do the results mean in practical terms?
The 'Diversity-Stability Debate' (McCann, 2000) tries to get closer to the fundamental, and current, question of whether the stability of an ecosystem improves or deteriorates when individual species are removed from the network, e.g. through human exploitation of resources. We conclude from our study that there is no easy path towards ecosystem theories that settle the diversity-stability debate. Rather, the evolutionary path followed by species in an ecosystem cannot be 'short-cut' by simplifying towards randomly composed interactions. Our study picks up on a current aspect of the sustainability debate.
Does it mean that all models of ecosystems calculated with random matrices are wrong?
It is generally the case that no model is 'right'. There are models that are useful because they help understand nature better. We argue here that random matrices are not sufficient to describe the stability of species networks when these species have been adjusted to each other through an evolutionary process.
To what extent are these new findings relevant to society?
The stability of ecosystems is a topical issue, especially because humans are responsible for often severe disturbances to existing ecosystems and can hence affect the stability of ecosystems. This can be seen, for example, in the loss of biodiversity, when species richness is in fact essential for ecological balance. With our new approach to modelling, we shed new light on the question of how complex ecosystems reach a state of equilibrium.
Publication:
Låstad, S.B., Haerter, J.O. The geometry of evolved community matrix spectra. Sci Rep 12, 14668 (2022). https://doi.org/10.1038/s41598-022-17379-6




